The scientific problems I have worked on as a theoretical physicist are conceptualized by professional physicists within the language of mathematics. I think however that many of the ideas can be understood with a minimum amount of mathematics. I have resisted the best efforts of Alice for many years to try to explain to her in simple terms what it is that I do. Perhaps, after reading these pages, she will agree that my resistance reflected good judgement on my part. The account I give here is only that of the work with which I have been directly involved. The description will be largely metaphorical, but as much as possible, true. As with all metaphorical descriptions, some amount of compromise is made between various elements of truth, conciseness, imagery, and analogy. For any professional colleagues who are misfortunate enough to stumble across these pages: Have mercy on me! You may be foolish enough to try this sometime in your life.
Vacuum Polarization near Highly Charged Nuclei
This topic was the subject of my thesis at the University of Washington in 1975. The work was done with Lowell S. Brown, who was my advisor and on the faculty at that time, and Bob Cahn who is currently on the faculty of Lawrence Berkeley Laboratory.
Before I can explain what this project concerns, I need to give an explanation of some basic elements of quantum mechanics. Quantum mechanics postulates that the classical description of matter proposed by Newton is fundamentally flawed. Newton assumes that to each particle of matter we can assign simultaneously a time, position, energy and momentum. (Energy and momentum are not independent since if we know the mass and momentum of a particle, we also know its energy.) Quantum mechanics treats matter in a fundamentally different way than does Newtonian mechanics: Particles are not well localized, and are described by probability waves. These waves are somewhat analogous to waves of light, except that particles move with less than light speed. Constructing a well localized wave at some position and some time is not easy to do, as a large uncertainty in its momentum and energy is introduced. Conversely, waves of well defined momenta and energy are always well spread out in space and time. This inability to simultaneously localize a particle and specify its energy and momentum is summarized in the Heisenberg uncertainty principle:
The first relationship is that the uncertainty in the position times the uncertainty in momentum must be greater than a constant, h, which is a universal number, called Planck’s constant. The second relation is that the uncertainty in energy times the uncertainty in the value of time is also greater than h. These equations mean for example, if we have a very small uncertainty in the position of a particle, then its momentum has a very big uncertainty. Or if we have a very small uncertainty about the time at which a particle had an interaction, we then have a very large uncertainty in its energy.
This has an amusing consequence: For short time scales and small distance scales, energy and momentum need not be conserved. Of course, this all gets fixed up on long time scales and large distance scales when one has averaged over many fluctuations, so the non-conervation cannot be used to make a perpetual motion machine.
Physicists like to conceptualize matter in terms of states which have various numbers of particles in them. These are particles which can exist for very long times and travel over large distances, so on such scales their energy and momenta are well defined. There is a special state, the vacuum, that has the lowest energy of all states, and contains no long lived particles. There can be no particles in this state, because they would have energy and the vacuum is the lowest energy state. (Even a particle which is not moving has some energy because Einstein taught us that mass is equivalent to energy.) However, there can be very short lived fluctuations of the vacuum which are allowed to happen, because energy is not conserved on very short time scales. Physicists think of the vacuum state as containing lots of fluctuations of particles occurring over very short time scales. They also occur over very short distance scales because the uncertainty in energy implies an uncertainty in momenta. The typical time scales involved for these fluctuations are of the order of the time it takes light to fly across the size of a particle, which for an electron, is about
One way to see the effects of such fluctuations is to apply a strong electric field. If electrons generate the fluctuations, then they must appear in electron-positron pairs because electromagnetic charge must be conserved. A positron has the opposite charge to that of the electron, so that a pair has no charge. The positron is the antiparticle for the electron and has the same mass and opposite charge. If these pairs appear in the presence of a strong electric fields, they will affect the electric field, because the pairs can also generate an electric field. These pairs and their modification of electric or magnetic fields is called vacuum polarization.
At the time I wrote my thesis, Walter Greiner at the University of Frankfurt had been studying the effects of strong electromagnetic field on the vacuum. In principle, we have a complete description of electromagnetic physics using the mathematics of the theory Quantum Electrodynamics.
Electrodynamics means simply the dynamics of objects which can generate electric and magnetic fields.
Quantum means that the theory is includes the probabilistic and wave nature of matter. Prior to Quantum Electrodynamics, people used classical electrodynamics which used the older ideas of Newtonian mechanics. Quantum Electrodynamics describe electrons, positrons and photons. It also describes the interactions of protons and neutrons, the constituents of atomic nuclei at distances much larger than the sizes of protons and neutrons. At smaller sizes, the quark substructure of matter becomes important, and their are new forces besides electromagnetic, which need to be included in a theory.
Dirac was the first to write down an equation to describe relativistic electrons. He was surprised that there were two types of solutions. One solution has positive energy and is the electron. The other solution has negative energy. This solution could create many problems, since a positive energy electron could lose energy indefinitely spiraling down into a more and more negative energy state. This would mean that matter is fundamentally unstable. Dirac and Feynman solved this problem by arguing that the vacuum was filled with negative energy states from zero energy all the way down to negative infinite energy. The reason the electron cannot spiral down into these sates is that they are occupied. Years before Pauli had argued that electrons satisfy the now named Pauli exclusion principle: No two electrons can occupy the same state.
This does not mean that the filled negative energy states, now called the Dirac Sea, have no effect: If you remove a particle from the Dirac sea, the absence of the particle appears as if there is a positive energy particle with charge opposite to that of the electron. A particle can be swallowed by a hole, losing its charge. It is said to annihilate against the oppositely charged antiparticle. Because it takes a positive energy to make such a hole the antiparticle has positive energy. This construction led to the idea of anti-matter, and predicted the antiparticle partner of the electron: the positron.
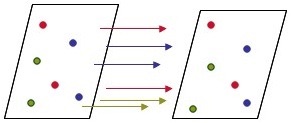
The Dirac-Feynman construction is shown in the figure below. Filled circles represent filled states. Open circles represent unfilled states. We should imagine the possible energy values going to arbitrarily large negative and positive values. The figure on the left is the vacuum. In the middle, there is a single electron. The figure on the right corresponds to a negative energy hole or a positive energy electron
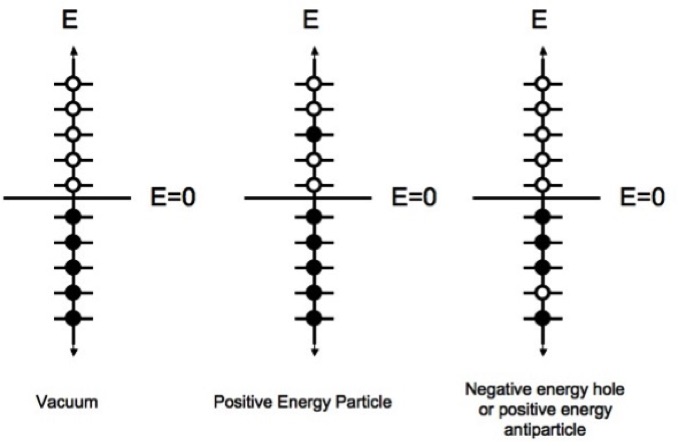
In the picture above, we could imagine a state with one particle of positive energy and one hole of negative energy. Then the particle might fill the hole making a vacuum state. Energy would be released, and this would appear in the form of photons. This was one of the predictions of Dirac, that there should be electrons and positrons and they can annihilate.
The issue that interested Walter Greiner was how the vacuum behaved in very strong electric fields. For example, if you have a highly charged nucleus, the field can be very strong. The strength of such fields are parameterized by the number of positively charged particles in the nucleus Z, times the fine structure constant. The fine structure constant is a number whose value is about 1/137. If one had a nucleus with Z much greater than 137, the fields would be really strong. Unfortunately, the number of positive charges in a nucleus is naturally limited by about Z ~ 100 so it is not possible to make the fields extremely strong. The best that can be done is in collisions of heavy nuclei where for a brief time when the two nuclei overlap they generate an electric field as if they are one nucleus with a Z as large as 200.
When Z is about 150 or so, a very interesting thing happens. The energy of an electron bound to an atomic nucleus becomes negative, and so a positive energy state becomes a negative energy state. The nature of the vacuum changes.
This suggests that one might learn something interesting about the vacuum structure of nature by studying how vacuum polarization modifies the electromagnetic field of very highly charged nuclei. In particular, one might expect significant modifications of an electric field due to vacuum polarization from electron-positron pairs flickering on and off in its field.
My thesis was not the first work on this problem. There was previous work by Wichmann and Kroll, who computed the effects of vacuum polarization for nuclei in the approximation that the nucleus has zero size. We repeated their computations and got an elegant and simple “analytic result” in the limit when we looked at the electric field at distances very small compared to the size of an electron. Analytic results are important for theoretical physicists. An analytic result is one that you can write down in terms of known functions. Much is known about the properties of such functions, and sometimes analytic results have a beautiful mathematical structure. It also means that you know much about the result without ever having to use a computer to do a numerical evaluation. We also computed the effects of finite nuclear size.
One of the side benefits of this computation was that I made lifelong friendships with Walter Greiner and his group at Frankfurt, and with Miklos Gyulassy who was a student at Berkeley at that time. Miklos and I have shared many common interests in physics over our lifetime, stemming from our common interest as graduate students. Miklos had developed powerful numerical methods to compute the effects of finite nuclear size. Our analytic and his numerical results agreed.
I also learned to respect hard computations, and that to make progress one needed to find a good
approximation. Ours was to consider distances small compared to the size of an electron. In almost all of the problems I have worked on, I have always been able to make some approximation which lets me solve the problem. A well defined approximation is even useful when it does not work. It lets you imagine an ideal world where the approximation does work, and you can solve that problem. Once the problem for the ideal world is solved, you may be forced to revise your thinking about the real world, and that revision oftentimes leads to progress in new directions.
Perhaps the strongest effect of this work was that I learned about some of the magical aspects of theoretical physics. After working many, many weeks trying to solve equations, I would find that at some point they would all collapse to simple results, if I was doing the computation correctly. If I made some dumb mistake, the results would never collapse and I would be left with ugly looking formulae that could not be written on a single sheet of paper. I strongly believe that there is a simplicity and elegance to the mathematical formulation of the laws of nature that goes beyond what one can explain with rational or logical principles. I sometimes scandalize my colleagues when I lecture to freshman physics classes, and I begin the course by trying to teach young people this principle of magic. I strongly believe that science has aspects of magic, but not superstition.
Some physicists take this a bit too far, however. There is a class of theorist who believes that he or she can write down the laws of nature on the basis of pure thought. The guiding principles are elegance and logical consistency. I find this philosophy a little troubling. I have always believed that if anyone has free will to define the laws of the universe it is God. There should be alternative universes that one can imagine where the laws of physics are both elegant and simple, and man can simply not realize them.
My friend Bob Jaffe puts it in a little more simple terms. He says that we could perfectly well live in a world described by Newtonian mechanics. Newtonian mechanics is certainly simpler and more elegant than Quantum Mechanics, yet we know that Quantum Mechanics is the correct description. Perhaps at this point the skeptic might argue that it is precisely the uncertainty of quantum mechanics that is the manifestation of God’s free will.
As a practical matter, I rarely think in these terms. I think I am more of the “Little Steps for Little Feet” philosophy, and have not ventured so far into the night as have some of my colleagues.
Properties of Quark Matter
On my first postdoctoral fellowship at MIT, Ken Johnson got me interested in the properties of strongly interacting matter at extremely high energy densities. Problems related to the properties of matter at energy densities much larger than occur naturally in atomic nuclei have been the central focus of my career.
Strong interactions are responsible for the nuclear force. They arise from the quark and gluonic constituents of a subset of particles which interact strongly. These particles that interact strongly are called hadrons, from the Greek word Hadros which simply means strong. Quarks and gluons carry a charge called color, and when they interact, they exchange colored particles, changing their own color. Quarks are the basic constituents of ordinary matter like neutrons and protons. The theory of strongly interacting quarks and gluons is called Quantum Chromodynamics (QCD), that simply means the quantum interactions of colored particles. QCD is a theory of quarks with three colors, Nc = 3.
QCD has the remarkable property that when distances are large, interactions become very big, and conversely, when distances are very small, interactions are very weak. This requires that all the states which can naturally occur have zero net color, since otherwise it would take an infinite amount of energy to produce the state. To understand this, imagine we tried to make a state of two widely separated particles by moving apart two colored particles which were originally in a well localized colorless state. The interactions would become huge as we pulled them apart, and this would require much work. As we pulled them to infinite separation, an infinite amount of energy would be required.
For a theory of quarks with three colors, Nc = 3, it turns out that the only colorless states are those with
a difference of quark and antiquarks equal to an integer p times the number of colors
If p = 0 in this equation there is no net number of quarks, and such states are called mesons. If p = 1, the difference in quarks and antiquarks is three, and such states are called baryons. Baryons are the protons and neutrons which compose atomic nuclei. Mesons are short lived states which are produced in the interactions of baryons. States with p > 1, are multiple baryon states. States with p negative are anti-baryonic. The property of QCD that only color singlet states can occur in nature is called confinement: Isolated quarks can never appear in nature since they are colored, so they are permanently confined inside of color neutral hadrons.
The idea behind Quark Matter is that if you take ordinary matter and squeeze it to densities greater than that of atomic nuclei, then individual baryons become so squeezed that there is no space left between them. It might be reasonable to expect that the quarks which compose these baryons can now move freely about the entire matter, and are no longer confined into individual baryons. Such high energy density matter actually occurs in neutron stars, where energy densities an order of magnitude larger than that of atomic nuclei occur. Neutrons stars are made from dying stars that cannot generate enough heat to make a big enough pressure to resist gravitational collapse. The original star collapses to an object of size about 10 kilometers. It is held up by the effect of the Pauli exclusion principle, which prevent identical fermions from occupying the same state. (Eventually even the Pauli pressure cannot support the star as more and more matter is added, and it will collapse into a black hole.) High energy density matter can also be made in the collisions of atomic nuclei in accelerators. Quark Matter coalescing into neutrons and protons is shown in the illustration below
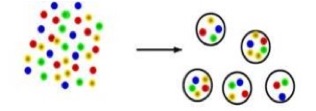
The idea that Quark Matter might form by compressing protons and neutrons (referred to collectively as nucleons or “ordinary baryons”) was suggested in 1970 by Naoki Itoh, before I had even entered graduate school. Peter Carruthers had made similar speculations a little later. The reason why I was interested in Quark Matter was because we now had a theory of quark and gluon interactions, and as observed by Collins and Perry in 1975, such quarks and gluons should be weakly interacting at high density, because the typical distance scale between quarks and gluons would be small, and interactions get weak in QCD if typical distances are small. A similar observation about the properties of matter at high energy density had been independently made by Cabibbo and Parisi at about the same time. This meant that one could compute the properties of a strongly interacting high energy density gas of quarks and gluons from first principles. While we were setting up our computation, Baym and Chin at the University of Illinois had computed the first effect of interactions. Together with Barry Freedman, we computed the effect of interactions to a high enough order so that we could see the interaction become weaker at high energy density. (The order of a computations is how many powers of the interaction strength has been included. First order mean that the effect of one interaction for each particle is included. Second order mean two interactions, etc.) This was the first computation of any type done in QCD of a physical process at high enough order so that one could see such effects. Many people at the time believed that such computations were in principle impossible since there would be uncontrollable infinities associated with interactions at large distances. It as a very hard and long computation, and I was very lucky to work with Barry who had the attention to detail, and sheer mental muscle, to properly do this computation
We also set up a framework for computation not just when the density of baryons became large but also when the temperature became large. We did not pursue this, but in 1978 Edward Shuryak did the first high temperature computation, followed closely by Joe Kapusta. Edward gave the name Quark Gluon Plasma to the Quark Matter when it also has finite temperature. The phrase Quark Gluon Plasma is more commonly used to describe high energy density Quark Matter, but the major conference in the field still refers to itself as Quark Matter.
The computation took us about a year to complete. It was very difficult because we did not have established techniques of computation and we were overly cautious about possible infinities from long distance effects. A short while later, Varush Baluni confirmed our results. Nowadays, computations have been done which include much higher order effects, and are done in much less time.
The De-confinement Phase Transition
In the late 1970’s, Ken Wilson proposed an idea which might allow one to compute the properties of Quantum Chromodynamics using numerical methods on a computer. Quantities which can be measured in QCD have a representation as a sum over all possible values of the color electric and color magnetic field, fields that are analogous to the electromagnetic fields of electromagnetism. In addition, a sum also has to be done over fields associated with the quarks. Computing this sum over all possible values of a field is very difficult. What Wilson showed is that one could write the theory on a discretized lattice of space-time points. Then one did ordinary sums over numbers associated with the values of the fields at these space-time points. One could also write the theory in such a way that these sums could be approximated by methods of selective sampling. This selective sampling is called Monte-Carlo integration, since it is a bit like gambling, in that you are making educated guesses about what are the dominant contributions to control the outcome. This way of thinking about doing computations in QCD became known as lattice gauge theory. It is now a huge business.
Ken Wilson did not think that these methods were practical on the size of computers we had in the 1970’s, but Mike Creutz was very brave and tried them anyway. Mike demonstrated some amazing results: He showed for the first time that QCD had the property of confinement, and that the energy of separation of two color charges would grow linearly as the separation increased. These results were for small systems, and much of the progress over the past 30 years has been to develop methods to handle larger and larger systems. Some people say Mike never proved confinement, and in a strict mathematical sense this is true, but what he did is good enough for me.
I was attending the Gordon Conference on particle physics in the summer of 1979. Mike Creutz was also at the meeting and he told me about his breakthrough. He was trying unsuccessfully to get his talk on the agenda of the meeting, but the organizers did not understand what he had done. When I found out what he had done, I was really excited, and I could not understand why everyone did not stop what they were doing and go off and calculate using lattice gauge theory. Mike had made punch card copies of his computer program, and gave me a copy, which I carried off to the Stanford Linear Accelerator Center where I was then a postdoctoral fellow. I invited him out to give a seminar at SLAC after consulting with senior colleagues at SLAC, who also got very excited.
The phenomena where someone makes a big discovery in physics, and for some time it goes unnoticed is common. It takes time for people to understand the scope and impact of new ideas. Physics is ultimately a very fair science. Good ideas do get recognized, and almost always, credit is fairly given, but it takes time.
At SLAC, there was this very bright student Ben Svetitsky. I knew he was brilliant because two of the fastest minds in the group, Helen Quinn and Marvin Weinstein, would talk with Ben, both speaking at an incredible rate, and Ben could intelligently follow both conversations at the same time. They were working on aspects of lattice gauge theory using techniques to increase understanding, but which were not useful for Monte-Carlo computation.
Ben and I started talking and we decided we would use Monte Carlo methods to try to see if there was a phase transition between a confined and an unconfined phase of QCD. What this means is that there are two different ways that nature could manifest itself. One is the confined world in which we live. Another is a world where quarks could move around freely, not confined inside a specific hadron. This might occur for systems of high energy density, as had been suggested by Collins and Perry and by Cabibbo and Parisi. A phase transition is a discontinuous change between these two worlds.
There were arguments that such a phase transition might occur. Work by Polyakov and Susskind had shown that there was an order parameter for such a transition, which was essentially the energy of an isolated quark. If it is infinite, there is confinement, and if it is finite, there is not. They had provided plausible arguments about why there might be a phase transition.
We therefore generalized the methods Mike Creutz had used for computing the properties of isolated particles to a system of quarks and gluons at finite temperature. We decided to compute the energy of an isolated single quark. After a lot of missteps, we found that there was a phase transition, and we estimated its temperature.
Our computation was on a very small lattice, that is we made a poor approximation to the real world. Our theory was for 2 colors of quarks and not the three we live in, and in fact we did not even allow quark-antiquark pairs to be produced. You get to be so carefree only if you are the first to do something. We were technically first to publish, but in fact, at the same time, Kuti, Polonyi and Szlachanyi were doing the same computation. Our results appeared back to back in Physics Letters.
Nowadays, computations of the properties of matter at finite temperature are very sophisticated. They involve huge computers, large lattices, use the correct number of quark colors, and even include quark-antiquark pairs. There are elaborate methods to extrapolate to truly huge systems. My good friend Fritjof Karsch always jokes that the only thing Ben and I did right was to get the correct answer.
There are worse things.
Centauros
During my time at Stanford Linear Accelerator Center, I was lucky to get to know and work with James Bjorken, known to most people in the physics world as Bj. Bj provided the insight which led to the direct measurement of the quark substructure of matter in electron-proton scattering. He and Feynman also provided the basic ideas about how quarks and gluons appear in generic high energy interactions. These ideas had tremendous impact on both elementary particle physics and modern nuclear physics. Bj is an unassuming low key man, who thinks intuitively, and whose intuition transforms itself into deep mathematical realization. I was a young postdoctoral fellow while at SLAC and my education had been mathematical. Bj’s way of thinking transformed not just the way I thought about various physics issues, but allowed me to think about new issues I would not have been able to properly envision.
The problem we worked on was a small one, related to a problem in cosmic ray physics. Cosmic rays are particles bombarding the earth from outer space. The high energy cosmic rays have origins outside our solar system. Cosmic rays provided some of the first tests of theories about interactions of particles at high energy, the existence of anti-matter, and a variety of new phenomena. The problem with cosmic rays is that the number of events one can measure is limited, and one cannot know precisely the energy and other properties of the beam of cosmic rays streaming down on the earth. Most interactions also take place after a cosmic ray has had many interactions in the atmosphere, that is before it hits a detector. Many phenomena have been discovered in cosmic rays which were not taken seriously because many other phenomena were discovered that were not true.
Nevertheless, cosmic rays physics and the people who do it are really fun. This area has been and continues to be the wild west of high energy physics. Just look at the recent excitement over the results from the Auge experiment showing very high energy cosmic rays tracing back to black holes in the centers of galaxies. This may be the birth of high energy astronomy, and there is a tremendous potential for discovery. Even if results are sometimes wrong, Bj taught me that it is good since you are forced to think about physics in new ways.
Bj had been bothered for some time about an anomaly in mountain top cosmic ray experiments. At mountain tops, cosmic rays have interacted many times, and a nucleus has certainly broken up into its nucleon constituents before reaching such low depths in the atmosphere. There were a class of events called Centauros that looked in part like a nucleus breaking up above the experimental apparatus. It could not be a nucleus, since nuclei do not penetrate that deeply into the atmosphere, and there were some other puzzling features. All of this might be explained if the matter was highly compressed quark matter.
We conjectured that maybe at the top of the atmosphere, a nuclear interaction had made a glob of metastable quark matter which was more tightly bound than nuclei. This matter had such high density that not only were there ordinary quarks in it which make up the neutron and proton, but there were in addition strange quarks, which are associated with more exotic baryons. The strange quarks make it a droplet of strange quark matter.
A little before us and independently, Kerman and Chin were suggesting the same mechanism. Later, Witten at Princeton made the radical and clever assumption that strange quark matter might be absolutely stable compared to ordinary nuclei. There were no strong arguments that this should be the case, but more surprising, there were not strong arguments that it was not the case. If true, stable strange quark matter means that all ordinary nuclei would eventually decay into strange quark matter.
This might have all manner of horrible consequences, but it turns out no to be dangerous since there is a barrier to the formation of strange quark matter for charged particles, and all stable nuclei are charged, so the rate at which such processes may happen are tremendously small, so small that it will never happen in our universe.
Stable quark matter has been looked for in experiments at CERN and at BNL. With very high confidence this matter not been seen. The possibility of metastable quark matter still remains, but even the experimental data which originally suggested Centauros has been reanalyzed, and the events have disappeared.
Ultra-relativistic Heavy Ion Collisions
Toward the end of my stay at SLAC in 1980, I became intrigued by the possibility that in heavy the collisions of nuclei at very high energy, one might be able to produce and study new forms of matter. This was not a new idea. T. D. Lee an G. C. Wick had proposed about five years previously that one might be able to use such collisions to heat up the vacuum, and perhaps make a transition to new phases of matter. The new thing I brought to the table was the insight I had learned from Bj about how high energy strongly interacting particles behaved. Bj, Feynman and Gribov are fathers of the parton model. This model provides a schematic picture of the space-time evolution of the matter produced in heavy ion collisions. It tells you typical spatial coordinates and times at which matter is formed in high energy collisions.
A high energy collision of two ultra-relativistic nuclei begins with the two nuclei heading to one another at near light speed with equal and opposite momentum. The nuclei are highly Lorentz contracted, they each carry tremendous energy. Their internal dynamics is frozen in time because of Lorentz time dilation. An essential part of the argument by Bj, Feynman and Gribov is that because of Lorentz time dilation, the nuclei themselves will not feel the effect of any collision until much after the collision takes place. They fall apart at times much after the collision occurs.
Particles are produced with a wide range of momenta in the collision. Some are not moving very fast after the collision, some have momentum close to the nuclei, and there is a range of momentum in between. (The typical momenta of particle perpendicular to the direction of the collision axis is small.) Those particles with small momenta are produced immediately after the collision, because there is no Lorentz time dilation to forbid their production. The particles with higher momenta are produced later,
because they have a bigger Lorentz time dilation. They are also produced farther from the original collision point because they travel faster. This is the so called inside-outside cascade as named by Bj. It is shown in the figure below.
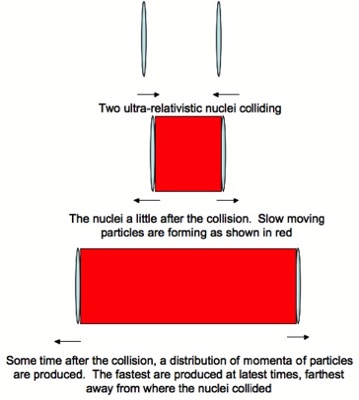
If you know from experiment the typical distribution of particles as a function of momenta, these arguments allow you to determine the energy density and number density of particles immediately after they are produced. I was really helped in my understanding of how this works by papers by Andrzej Bialas. He had simple arguments about the space-time distribution of produced particles in proton-nucleus collisions, and simple arguments about the relationships between proton-proton collisions and proton nucleus collisions. I still remember how excited I was when I would understand the arguments in Andrzej’s papers. They were so simply made, but so powerful.
In 1979, I put together a collaboration with Ramesh Anishetty, a student from the University of Washington who was visiting me at SLAC, and with Peter Koehler, a young scientist visiting on a German fellowship. Together we understood how the parton model worked for ultra-relativistic nuclear collisions. We estimated the energy density and particle number densities in the region where the nuclei sat. At that time, estimating what happened in the region between the two nuclei was much more speculative, but in conference proceedings, I presented results under various assumptions.
There had been previous work on the energy deposition in proton-proton collisions by Edward Shuryak in 1978. Some features of what he had done are included in our analysis. (I was not aware of Edward’s work until much later, and we did not cite it in our paper as we should have.) We liked nuclei better since the study of properties of high energy density matter is much simpler if the typical size of the system is large compared to the typical particle separation. This is largest for a nucleus, since a nucleus is much bigger than a proton. The energy and particle densities are also larger for nuclear collisions because a higher density of particles is produced in nuclear collisions than in proton collisions. Edward’s work nevertheless showed deep physical insight, and was in fact the first to argue in a modern context for high energy collisions as a tool to study forms of high energy density matter.
I remember that I had the results of this paper together with the first results from the lattice Monte-Carlo simulation of finite temperature Quantum Chromodynamics when I went on my first trip to Europe. Helmut Satz had organized a meeting at the Center for Interdisciplinary Studies at Bielefeld on the topic of high energy density matter. I successfully convinced Helmut to include the work about finite temperature QCD on the agenda, but he could not fit the talk on high energy collisions. Nevertheless, Keijo Kajantie and I began talking, and Keijo got interested. More about this meeting, and the friendship with Helmut and Keijo is described in the anecdotal vita.
In 1982, Bj became interested in the problem of ultra-relativistic nuclear collisions and wrote a very famous paper. He used his parton model description to generate initial conditions for fluid dynamics equations which describe the subsequent evolution of the produced matter. He then solved these equations for the types of energy density pressure relationships one expects for Quark Gluon Matter.
Bj also had a stroke of genius in the way he formulated the issue of the energy density. He wrote down an equation for the energy density one would infer at a very early time in the collision directly in terms of experimentally measurable quantities. I have always kicked myself that I was not clever enough to do this. I knew and understood all of the ingredients of the relationship, and the result was implicit in what I had done, but I simply did not make the next step.
After the paper with Anishetty and Koehler, Keijo Kajantie and I began collaborating. We generalized Bjorken’s considerations somewhat. With Miklos Gylassy, Keijo and I understood how phase transitions might generate expanding nucleation bubbles and explosive behavior. This took us back to the work of Zeldovich who years ago had evolved a theory of chemical explosions within fluid dynamics. Together with Keijo and Vesa Russkanen, Henrique von Gersdorff and young Finnish colleagues, we developed a fluid dynamic treatment which allowed us to treat nuclei of finite size. The treatment by Bjorken had assumed infinite sized nuclei. This let us compute a number of potential experimental signatures of the production of a Quark Gluon Plasma. One of my best works at that time was with a young Finnish student who visited me at Seattle for several months, Tuomo Toimela, and involved a fairly complete first principles description of the production of electromagnetic particles (particles which interact only through their electromagnetic force, and do not have strong interactions.) (My appreciation for Finnish theoretical physics is very strong, developed at that time and continuing to this day, and I am very proud to be a foreign member of the Finnish Academy of Sciences.)
This was a time of intellectual exploration. The broad outlines of how to think about ultra-relativistic nuclear collisions had not been developed, nor the ideas about what to look for to measure properties of a Quark Gluon Plasma. It was exciting because there were very few people had thought about such problems, and so very little had been explored. Nowadays this is a very sophisticated field, and one does a very good job of describing what takes place in these collisions. There are now signatures of the Quark Gluon Plasma, and a few years ago, at Brookhaven National Laboratory made a public announcement of discovery. This is the result of huge worldwide theoretical and experimental efforts. There is a recent summary of the situation in my 2005 paper with Miklos Gyulassy.
Baryon plus Lepton Number Violation in Electroweak Theory
When I was at Fermilab at about 1986, I became interested in the problem of baryon and lepton number violation in electroweak theory. Baryons are particles like the neutron and proton which constitute nuclei, and leptons are particles like the electron and neutrinos. Electroweak theory is a theory proposed by Glashow, Salam and Weinberg to unify the description of electromagnetic forces and a class of weak interactions among elementary particles. In addition to quarks, gluons and leptons and photons, it also has electroweak W and Z bosons.
This was because of a couple of very interesting, and at the time controversial, papers by Nick Manton, Frans Klinkhammer, Vadim Kuzmin, Valery Rubakov and Misha Shaposhnikov. When you first hear this idea, it sounds completely crazy. The theory of electroweak interactions had been written down in a way to explicitly conserve baryon number. The Maxwell equations of electroweak theory tell you that as you evolve electroweak fields, you never change the baryon number or lepton number. I started out thinking that this was nuts, and ended up concluding that it was most reasonable.
The original idea that electroweak theory might have baryon number violation came from ‘t Hooft. ‘t Hooft computed the rate at low energy in 1978. He argued that while electroweak theory conserved baryon number in the Maxwell equations which described the electroweak fields, baryon number was not conserved when quantum effects were included. He computed the rate but it was so small that it might have happened a few times in the entire volume of the universe during the entire time the universe existed.
The way that the ‘t Hooft mechanism works can be understood in the figure below. In the top part of the figure, there is a plot of the energy of the electroweak fields, called the potential V, versus Q. Q is called a Chern-Simons charge. V is called a potential because it is a potential energy stored in fields. The potential is periodic and that means if we move by a certain amount in Q, we get the same value of the potential. The Chern-Simons charge is designed so that the changes which make the potential the same are integers. Now suppose nature chooses the vacuum state and the red ball in the figure, that corresponds to the electroweak fields, sits at the minimum where Q = 0. We could of course imagine moving the fields to a new minimum. say the one to the right where Q = 1, as shown in the figure. The minimum at Q=1 is just as good as the original one at Q = 0. In fact all the properties of nature which would arise from the theory at Q = 1 would be the same as would be for Q = 0. In particular, all of the possible energy values for a Dirac particle like an electron or a quark would be the same for either Q = 0 or Q = 1. This is because there is a invariance of nature under an integer difference in the Chern charge, and this invariance comes from a symmetry of the theory. Of course when we move the ball from Q = 0 to Q = 1, we go through values of the Chern-Simons charge which are not an integer, but in the end, we end up with an integer value and we would think nothing could have happened. This turns out to be not quite true!
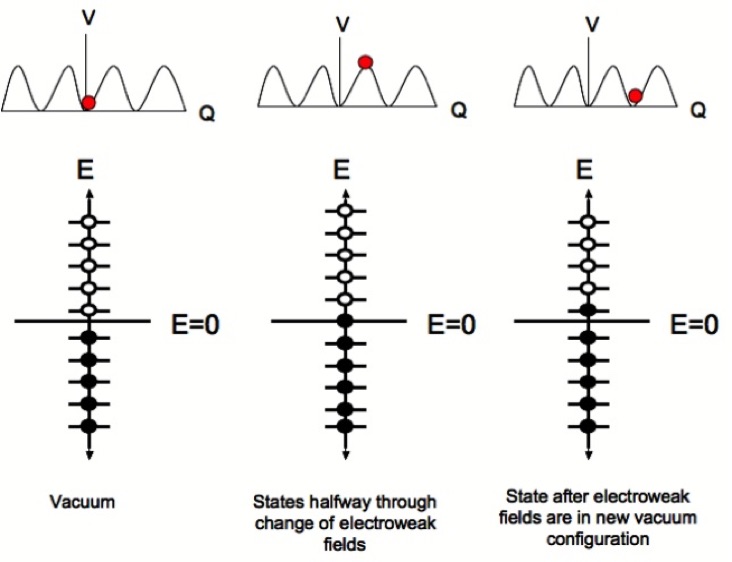
Remember in the discussion above, I explained how Dirac and Feynman quantized a theory with Fermions, that are particles like electrons and quarks. One has to fill up the negative energy Dirac sea. In the figure above, you see what happens to these energy levels as we take electroweak fields with Q = 0 to fields with Q = 1. The energy levels all continuously shift up by one unit as we move the ball. In the end, the energy levels are all the same, but because the negative energy states were all occupied, when we change the Chern-Simons charge, we end up with an occupied positive energy state. A positive energy state corresponds to a real particle. The change in Chern-Simons charge results in the creation Fermions! In electroweak theory, this corresponds to a production of baryon number, and lepton number. Lepton number counts the number of electrons and some other particles like neutrinos which do not have strong interactions and are fermions.
What ‘t Hooft discovered was that if one computed quantum mechanical transition of the electroweak fields, then there would also be a production of baryon number. Unfortunately the rate is very small.
Manton and Klinkhammer suggested that the situation might be different at high temperatures. At very low temperatures, it is very hard to make a transition between two minima with different values of the Chern-Simons charge. This is because the typical energy scale is very low at low temperatures and there can only be a quantum mechanical transition. If there is high temperature, however, thermal noise will cause transitions across the barrier, and if the typical energy scale is large compared to the barrier energy, the value of V when Q = 1/2 in the figure above, then the rate should be large. Kuzmin, Rubakov and Shaposhnikov provided a supporting arguments for this supposition, and a very nice picture of how the process can occur. They also suggested that such a process might generate the matter of the universe.
When Peter Arnold and I started thinking about the problem, there appeared to be many paradoxes associated with the understanding baryon number violation at high temperature. We sat down and did an explicit computation of the rate, and we found it to be large at high temperature (but perhaps not quite as large as previously conjectured, but large enough to be important for physics). Explicit computations are hard to argue about since if you do not make a mistake, the answer is what you have computed. We made no mistake. We later went back and wrote a paper resolving many of the apparent paradoxes with the thermal mechanism.
Peter was an incredible colleague. I would come to him with a half baked idea, which was usually wrong, and he would sit down and in a little time have an explicit “toy model computation” which would prove or disprove the idea. Toy model computations involve making some simplifying assumptions which render a result useless for numerical applications, but which have the essential ingredients of a more detailed computation. Making good theoretical toy models is an art, and much of what I have learned about such art comes from Peter.
Our work, and the work of Manton, Klinkhammer, Kuzmin, Rubakov and Shaposhnikov was very controversial, and most everyone thought we were crazy. The second paper with Peter where we addressed these issues was called “The Spheleron Strikes Back”. The sphaleron is a name given by Manton to mathematical object which appears in the computation. The title of our paper was taken after the Star Wars movie, and Physical Review would at first not let us use that title. Physical Review often confuses knitting clubs of little old ladies from Peoria with cabals of bomb tossing anarchists. (This confusion has sadly been often attributed to me and my colleagues.)
If baryon number is violated in electroweak theory, it might be responsible for generating the visible matter of the universe during the big bang. There are many simple properties of the visible matter energy density that are not understood from first principles. For example, the ratio of the number of baryons to photons, or the mass in dark matter compared to that in visible matter. It turns out to be not so simple to generate a baryon asymmetry in the big bang even if the laws of nature violate baryon number. I worked on a few mechanisms, one by myself and one in collaboration with Neil Turok and Misha Voloshin. Other mechanisms were suggested by a variety of people, most notable Misha Shaposhnikov, and Cohen, Kaplan and Nelson. It was established very early that some physics beyond the simple theory was needed. This is because to generate matter in the big bang, nature has to violate time reversal symmetry, and in ordinary electroweak theory, this is too weak in the conventional theory electroweak interactions, that is, the theory of Glashow, Salam and Weinberg.
I think it is fair to say that it is still not known whether or not the visible matter is generated by physics at an energy scale where electroweak baryon number violation plays an important role, or whether it occurs at another higher energy scale where there is unknown physics. A large reason for the uncertainty is that we do not yet fully understand the physics of electroweak interactions. Understanding this physics is the goal of the Large Hadron Collider at CERN in Geneva, Switzerland. This machine begins operations soon, and perhaps some light will be thrown on problems such as this.
After I went to Minnesota in 1988, I began working with Misha Voloshin and Arkady Vainshtein on the problem of baryon number violation for very high energy scattering of two particles. One would guess that such processes might be large if there was enough energy. Andreas Ringwald, then a student at Hedielberg, started such speculation with his computations of rates for such processes, which he found to be large at high energy. The initial conditions in high energy scattering are however very much different than those for high temperature processes. For high energy scattering, two particles scatter and make many. At high temperatures, many particles can scatter to make many. It turns out that this difference is important. The rates for high energy scattering turn out to be very very small. This took quite a long time to establish, and it is not at all obvious that it should be so, but sometimes a wrong initial hypothesis can prove to be an interesting one. Very good people thought about this problem, and I am convinced that the techniques learned from studying this problem are useful in other contexts. (One recent example where they have been useful is in considerations of black hole production.)
The Color Glass Condensate
While lecturing at the Crakow School of Theoretical School of Theoretical Physics in Zakopane in 1993, I attended lectures where recent data from the HERA experiments were being presented. These experiments involve the collisions of high energy electrons from protons. They can measure the distribution of quarks and gluons inside the proton. These quarks and gluons can have a range of energies from the energy of the proton down to a tenths of the rest mass of the proton. The ratio of the energy of a quark or a gluon to that of the proton is called x, and for HERA, the minimal value of x is
By making the energy of a proton higher and higher, one can look at smaller values of x. Understanding these low x gluons and quarks inside strongly interacting particles is equivalent to understanding the high energy limit of strong interactions. There is a very strong belief among theoretical physicists that this limit should be simple.
The low x gluons also control the interactions of protons and nuclei at high energy. If one had first principles understanding of the nature of this gluonic matter, then one would solve the long standing problem of the initial conditions for nuclear collisions. In the early studies of the matter produced in nuclear collisions, one started with somewhat arbitrary initial conditions at some not very well defined time after the collision had taken place. One was not able to ask what happened in the first instants of the collision. Clearly, the dynamics at that earliest times must have implications for what one measures in such collisions, and with a good understanding, one might probe with more precision the various ideas about the nature of matter at these most early time scales . At such very early time scales, the matter is most dense, and from a practical point of view, it seemed a little strange to ignore what took place, since the goal of heavy ion physics is to study the properties of matter at the highest energy density.
When I first saw the results from HERA, I was totally shocked. The number of gluons was rapidly rising as x got smaller and smaller. The high energy limit of strong interactions, QCD, therefore becomes the limit of high energy density matter. This is a profound philosophical difference form the way in which particle theorists would like to conceptualize high energies and simplicity: Simplicity for a particle theorist is the limit where there are only a few degrees of freedom. I understood from my experience in the theory of the Quark Gluon Plasma that this was not necessarily the case: Matter at very high energy densities could also have a very simple structure. However, this understanding is placed more within the realm of nuclear physics than of particle physics.
The observation that a rising number of gluons also means an increasing density requires also the observation that the size of a proton is not rapidly growing with energy. There are various bounds on the rate of growth, and it cannot be large, but from experiment, it is also known that the proton size grows slowly with energy. At the time the HERA results were presented, there was much speculation
about what would happen as the energy increased, and the most popular idea was saturation: That the gluon density would reach some limit, and then could grow no more. You simply could fit no more gluons into the proton. Ideas along these lines had been developed by Leonya Gribov, Levin and Ryskin and by Mueller and Qiu. But the gluon density in the HERA data just kept on growing.
I understood at the meeting that this meant that the high energy limit was a limit where the intrinsic strength of interactions, g, is weak. This is because of the remarkable property of QCD that at short distances, the interaction becomes weak. If the density of gluons is very large, the typical separation of gluons is very small. The problem becomes how to generate a rapidly growing distribution, and also deal with the saturation phenomenon. I also understood from my thesis work on strong Coulombic fields, that even though an intrinsic interaction is weak, if interactions act coherently, then one can drive big forces. If this was what was going on in the HERA data, it meant that the high energy limit of QCD was one which could be understood and computed from first principles in a weakly coupled theory.
To understand how inherently weak interactions can coherently add to a strong force, consider gravity.
The gravitational force between two protons is the weakest naturally occurring force. On the other hand, the force of gravity on me as I sit typing now, is the strongest force I feel. This is because the force of each proton in the earth pulls on each proton on me, and the forces all add together with the same sign (they are coherent). Because there are a lot of atoms in me and even more in the earth, a very large force results.
I was very excited by these possibilities when I got back to the University of Minnesota. Raju Venugopalan was a young postdoctoral fellow in our group, and we began sketching out ideas about how we could generate strong color fields in a proton at small x. Raju got us thinking about the light cone Hamiltonian methods of Stan Brodsky, and this proved a correct direction to follow. We first thought about a large nucleus, where we could treat the high x constituents of the nucleus as sources.
We found that for a very large nucleus, we could generate a large gluonic field at small x. We discovered that the sources for these fields could be treated as a random sum. The theory derived had many nice properties, and allowed us to compute properties of gluon distributions when the gluon distribution was large.
I have worked with Raju on many projects now. Raju is a quiet and modest man who thinks very deeply. He has a very broad and complete understanding of the breadth of particle and nuclear physics, that becomes apparent not through a showy display of bravura but by his mastery of the essential elements of a problem or presentation.
Our main breakthrough was to change the thinking about gluons from particles to fields. It is very easy to think about adding together the effects of fields, like adding the individual effects of a gravitational field from many protons to make a large total gravitational field. It is more difficult to do this with particles. Another example is an electromagnetic field. Two electric fields pointing in opposite directions will add together to make an electric field which vanishes. Therefore one will feel no effect of the sum of these two fields. On the other hand, two identical particles when they collide in succession, generate twice the impact. Fields can easily be treated as coherent, but particles cannot.
The coherence of the gluonic field allowed us to think about many phenomena in a new way, but not everything was solved. We still did not understand how the number of gluons rose as we went to smaller and smaller values of x. In the figure below you see a picture of a hadron at low energy and also at high energy. At low energy, a hadron effectively has only a few quarks and gluons and the density is low. At high energy the quarks and gluons get packed tightly together.
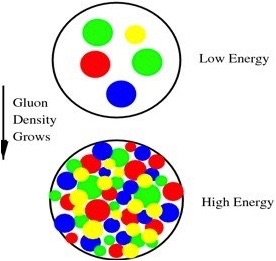
For gluons of a fixed size, the disk of gluons is tightly packed when the number of gluons per unit area becomes roughly equal to the inverse of the area of the gluon. The packing does not stop then, because the interactions between the gluons are rather weak. If the gluon size is small, then the interaction strength g is small. The packing actually continues until the density of gluons is so large that their coherent interaction strength slows the growth. It turns out that this happens when the number of gluons per quantum state is of order 1/g^2, which is big because g is small. Situations where the quantum occupation number is large happen in a variety of condensation phenomena in nature, such as Bose condensates, or superconductors or lasers.
Quantum mechanics also suggests that if we have a small object, its typical energy scale is large, since the uncertainty principle would give a momentum p ~ h/r, where p is the momentum scale a r the size scale. So as the disk fills up with gluons, it is energetically easiest to do using the largest gluons first, since they cost the least energy, After these gluon states are filled, one can move to smaller size scales. Also smaller gluons can easily pack themselves in amongst the larger ones. So as one goes to higher and higher energies, one can add more and more gluons but they need to be a smaller size scale, corresponding to a higher momentum scale.
The typical momentum scale where the gluons begin to be closest packed is called the saturation momentum. This continues to grow as the energy gets bigger and bigger. One of the consequences of our picture was that this simple description of saturation emerged.
We still did not understand why the saturation momentum continued to grow. In a collaboration with Alex Kovner, Jalilian-Marian and Heribert Weigert we understood how this might happen. (Along the way we corrected some early mistakes which had also been noticed by Yuri Kovchegov.) When Raju and I had described a nucleus, we had a clear idea that the quarks of the nucleus were the source of the gluonic field. If we look at small x, we need to include the gluons at a lower value of x as sources of the gluon field at yet lower values of x. This process of treating the gluons first as fields, and then as sources for lower energy fields leads to a mathematical procedure called a renormalization group. It allows one to actually determine the form of the sources of the gluon field at small x, and gives a growing value of the saturation momentum. These ideas were developed in the paper by Jalilian-Marion, Kovner, Leondiov and Weigert. They developed some truly beautiful mathematics. It turns out that the solution to the equation they write down has universal solutions, so the matter which one ultimately makes is the same if it was made by a nucleus or a proton. Universal quantities are the gems of physics.
Later I began working with Edmond Iancu and Andrei Leonidov on trying to get a clearer understanding of these results. We also corrected some small mistakes. and wrote two papers, the second also with Elena Ferreiro, which clearly explain the physics of the Color Glass Condensate. We derived equations which describe the properties of the Color Glass Condensate which are simple and elegant. In these papers we introduce this name. The word Color comes from the color of the gluons. The word Condensate is because the states we describe have high density of gluons and are coherent. The word Glass has its origin from the generation of the gluon field from fast moving sources. The sources are moving very fast and their time scales are Lorentz time dilated. The slow moving gluons associated with these sources then also evolve very slowly in time compared to their natural time scale. Systems which evolve slowly compared to their natural times scales are generically glasses. Ordinary glass is a liquid on long time scales but a solid on short one. If you are a physicist and want to have a good introduction to the field, the papers Iancu, Leonidov and me is a good place to begin. The papers are written in Edmond’s clear pedagogical style.
The words Color Glass Condensate were my invention. I think it took some time for many physicists to grow accustomed to them, and some have yet to do this. Until this name, people would describe this area of physics either by the tools which had been used to study it or by some mathematical object which would occur. For example, “Small x Physics”. These are not good names since they do not describe either an object one is trying to understand nor the goal of the work.
Edmond Iancu is the clearest thinking physicist I have ever had the pleasure to know. He also thinks very very fast. I am always humbled in my work with Edmond. Around Edmond, I feel like the Scarecrow in the Wizard of Oz: I wish I had been born with a brain. (He is described more in the anecdotal vita.) After these works together, we wrote a number of papers about the Color Glass Condensate. Because this is supposed to describe all of strong interactions in the high energy limit, the goals are very ambitious, and there are many things to consider. We described some general features of high energy electron-proton scattering with Kazu Itakura. With Genya Levin and Dima Kharzeev, we computed various aspects of particle production in high energy heavy ion collisions. Work by Jamal Jalilian-Marian, Kovhegov, Kharzeev, and Dumitru have predicted signatures of Color Glass Condensate in proton-nucleus collisions. With Yoshi Hatta, we showed that there were effective degrees of freedom of our theory which corresponded to objects long ago predicted in attempts to describe high energy scattering. With Elena Ferreiro and Kazu Itakura, we argued that the slow growth of the size of a proton as its energy increased had a simple interpretation because of the rapid growth of the density of gluons. There is now a wide and diverse literature on problems theoretical and related to experiment.
Another person who worked with me on properties of the Color Glass Condensate was Yuri Kovchegov. Yuri’s thesis at Columbia University was the first work to take seriously the ideas which Raju and I had proposed, and he found a few mistakes in the early treatment. I worked very hard to attract him to Minnesota where I was on the faculty. He is terrifically smart, creative and independent. At Minnesota, he did one of his most famous works, for which equations are named after him. Together, we understood some properties of high energy processes in which not many particles are produced. This was a fantastically fun collaboration, as neither of us suffer fools gladly, and neither of us likes to consider ourselves fools.
Yuri is a student of Al Mueller. Al and Genya Levin were two of the originators of many of the concepts of saturation. Both of them have made very important and prolific contributions to the general understanding of QCD. Genya developed many of the early ideas. Al also developed and implemented them, and his Dipole Model provides an alternative framework to the Color Glass Condensate for understanding high energy processes. One can show in all cases where they can be compared that they give equivalent results.
My good friend Peter Paul who is a most senior and respected scientist from Stony Brook, likes to tease me now about the Color Glass Condensate. At first, I think he was one of the few people who took the idea seriously. I think his friends made fun of us for our grandiose goals and for the name Color Glass Condensate, which some people felt sounded silly. Several years ago he told me that at first people laughed at the idea, but they have stopped laughing. That is OK, I guess. About two years ago, he told me it is now respectable science. I told him I hoped not, and that maybe I should work on something else. This year he told me it is part of history. That made me very depressed.
The Glasma
Several years ago, I gave a colloquium at a major university, one of the faculty told me that after he posted the abstract of the talk, a colleague had complained that there was typo in the abstract: I had misspelled Plasma as Glasma. The word Glasma was chosen to be a word halfway in between the Glass of the Color Glass Condensate and the Plasma of the Quark Gluon Plasma. The Glasma is produced when two very high energy sheets of Colored Glass collide and shatter. The fragments of this shattering are the Glasma, which eventually thermalizes into the Quark Gluon Plasma.
Shortly after Raju Venugopalan and I had formulated the classical field of the Color Glass Condensate, I understood that this would allow for a description of high energy scattering. Years before during a visit to Helsinki, I had thought about this problem with two young Finnish physicists, Harri Ehtamo and Juha Lindfors. We understood that many features of high energy scattering could be understood if in a collision, the two Lorentz contracted nuclei pass through one another and acquire charge. This was based on ideas of Low and Nussinov. There would be long range color electric fields generated and we proposed a simple guess for the initial field. It turned out that this guess had bad properties, and we could provide no good argument about how the nuclei could become charged when they passed through one another.
Alex Kovner and Heribert Weigert and I used the Color Glass Condensate fields in the initial wavefunction of two ultra-relativistic to provide the initial conditions for the fields which are produced in the instant of collision. It turns out this is a solvable problem, and it has the property that the two Lorentz contracted nuclei get dusted, instantaneously at the moment of collision with color electric and color magnetic charge.
Alex Kovner is now on the faculty of the University of Connecticut. He is very independent and almost iconoclastic. He is mathematically very strong and a very clear thinker. Heribert Weigert has made a number of important contributions to theoretical nuclear physics. He does not write many papers, but every one he has written is famous. There are few people with such high standards as Heribert.
We wrote down the equations which described the color electric and magnetic fields after the collision. The discontinuous change in the fields at the moment of collision is a big surprise. There are both color electric and color magnetic fields direct along the collision access, as shown in the figure below. A very high Chern-Simons charge density is generated, similar to that which occurs with the electroweak field in cosmology. In electroweak theory, the Chern-Simons charge was associated with baryon number violation. In the Glasma, it is associated with mass generation.
The equations which describe the time evolution of these fields can be solved numerically. This was done by Krasnitz, Venugopalan and Nara and by Lappi. Their results have a good phenomenology, and successfully predicted features of RHIC collisions.
I did not properly understand the nature of these fields at first. When giving a seminar about ten years ago in Lund, Sweden, Bo Anderson asked me how I could generate particles without big fields which pointed along the beam axis. Such fields are associated with Color Strings and the Lund String Model builds in these features. The Lund string model describes high energy processes very well. It turns out I had not thought about it carefully. A couple of years later, when visiting the University of Minnesota, in conversations with Joe Kapusta and Rainier Fries, I understood the depth of my lack of understanding, and realized the Glasma had both electric and magnetic fields of exactly the type that Bo had wanted. I went back to Brookhaven Laboratory, had a few conversations with Tuomas Lappi, a young Finn, and we wrote paper explaining the effect, and invented the name Glasma.
There are many issues which we still do not understand about Glasma physics. Perhaps the most important is how the Glasma forms a Quark Gluon Plasma. Strikland and colleagues have argued that there is an instability of these fields to make turbulence. Romatschke and Venugpoalan explicitly showed this instability is in the Glasma. Asakawa, Bass and Mueller have shown that such turbulence might explain some features of RHIC collisions. I, Francois Gelis and Kenji Fujikawa have argued that such instabilities may originate in quantum fluctuations of the Color Glass Condensate wavefunction. At this time, a complete description is lacking
I am very excited about the Glasma. The Glasma correctly generates all of the physics which Bj predicted in his parton model. Maybe it is also true.
Quarkyonic Matter
Recently my long term colleague and good friend Rob Pisarski wrote a paper together. This is a remarkable achievement. The paper is very good too. Rob and I are both alphas, and have resisted working with one another both for fear of the strength of the other’s personality. We had so much fun, we are now writing a second paper with Yoshimasa Hidaka.
The problem was to understand Quark Matter in the energy density-baryon density plane. Most people have thought that this was simply divided into a world of confined particles and deconfined. Maybe there are some other structures like superconductivity, but the main structure was confinement-deconfinement. We conclude that there is one more phase of matter.
We made a study when the number of quark colors is large. In the real world Nc = 3, so this might seem to be not such a good approximation. There is a wide literature on this, and the bottom line is that it should not be so bad. Corrections are typically of order 1/Nc^2 ~ 10%.
The first paradox to resolve is that in large Nc, no matter how high the density of quarks, quarks cannot affect confinement. Their effect on the gluons disappear in the limit of large Nc. This means that the confinement temperature is independent of the density of quarks. Therefore, cold quark matter is always confined.
As I described above on the section on Quark Matter, one can compute the properties of quark matter as if they were de-confined. On the other hand, if we consider the value of the baryon density, at low baryon density, it should be
(If you don’t like equations, the bottom line is that the density is very very small and vanishes as Nc becomes big.) Here I use that the mass of a baryon is of order Nc times a typical QCD scale, and I assumed temperature of the order of this QCD scale. Of course, if we include the effect of finite density, this baryon density becomes finite at some value, since we have to be able to allow for finite baryon number density systems. This means that there is a phase transition between a phase which has no baryons and a phase with baryons, both of which are confined. The confined phase with baryons however is best described in terms of quark degrees of freedom. This seemingly paradoxical situation can be resolved, but it required the existence of a third phase of confined baryons which behaves largely like a system of free quarks. We called this phase Quarkyonic, since it is somewhere between baryonic matter and quark matter.
That there is a new phase of matter is a radical idea and not yet understood in the community. They will.
The Chiral Magnetic Effect
My colleagues Dima Kharzeev, Rob Pisarski and Michael Tytgat invented the idea that there might be CP and P violation on an event by even basis in high energy nuclear collisions. P symmetry is the symmetry of the laws of physics under reflection in a mirror. CP violation is the same as symmetry of the laws of nature under reversal of time. Dima has argued the case for this elegantly and persuasively.
Dima is a truly gifted young scientist. He is unusual in that he has a smooth intelligence that allows him
to immediately understand ideas at an intuitive level. Most scientists struggle with mathematics before they are comfortable with an idea. Dima does this in the opposite order. He is the most like Bj of anyone I have met. He also has a clear understanding and enjoyment of the human comedy.
Together with Dima and a young Dutch physicist, Harmen Warringa we showed how this might explicitly happen in QCD. The effect is related to the anomalous baryon plus lepton number violation except for strong interactions. In QCD the effect is related to mass generation, not to baryon number violation. What happens is that if you change the Chern-Simons charge in QCD, you flip the spins of quarks relative to their direction of motion. Ordinarily such effects can only happen if there is mass, but changing the Chern-Simons charge can also do it. The Maxwell equations of QCD would not allow this and it is due to a quantum effect, like baryon number violation.
Suppose that there had been some Chern-Simons number charge generated by fluctuations. This could make a net polarization of the quarks along their direction of motion. If there was an external electromagnetic field pointing up, then positive charge quarks would have dominantly spin up and negatively dominantly down Since the quarks are polarized mainly along their direction of motion, the positively charged quarks mostly move up and the negatively charged ones mostly move down. Application of an external magnetic field results in an electromagnetic current parallel to the field. We call this the Chiral Magnetic Effect.
Such magnetic fields can be made in heavy ion collisions. The charges of the nuclei generate currents and these currents generate strong magnetic fields.
If seen, such an effect would be of great importance for the understanding of mass generation in QCD. It is a probe of anomalous processes associated with the Chern-Simons charge. It might throw light on the mechanism for the generation of visible matter in the big bang. If found, it is a big deal.